Fórmula de movimiento de proyectil
Tabla de contenido
En este artículo, busque la fórmula de movimiento de proyectil para un objeto disparado en ángulo y para el objeto disparado horizontalmente. Encuentre la fórmula relevante con ejemplos para una mejor comprensión. El movimiento de proyectil es una forma de movimiento en el cual un objeto o partícula (llamado proyectil) se lanza con cierta velocidad inicial cerca de la superficie de la tierra, y se mueve a lo largo de un camino curvo bajo la acción de la gravedad sola. Es un ejemplo de un movimiento bidimensional con aceleración constante. Un cuerpo se mueve en un movimiento de proyectil cuando se lanza en ángulo desde la superficie horizontal o cuando se dispara un objeto o se lanza horizontalmente desde el acantilado. Esto también se observa si un objeto se arroja en un ángulo horizontal desde el acantilado
Movimiento de proyectil de un objeto disparado horizontalmente desde la parte superior de la torre

Velocidad inicial Componente horizontal $ {v_ {0x}} = {v_0} $ Componente vertical $ {v_ {0y}} = 0 $ Aceleración horizontal $ a_x = 0 $ Aceleración vertical $ a_y = -g $ Ecuación de movimiento Coordenada X en cualquier punto $ x = {v_0} t $ Componente horizontal en cualquier punto $ v_x = {v_0} $ Coordenada Y en cualquier punto $ y = H – frac {1} {2} gt ^ 2 $ Componente vertical en cualquier punto $ v_y = -gt $ Ecuación de trayectoria $ y = H- frac {gx ^ 2} {2v_0} $ La trayectoria es una parábola. Tiempo de vuelo $ t = sqrt { frac {2H} {g}} $ Alcance horizontal del proyectil $ R = v_0 sqrt { frac {2H} {g}} $
Movimiento de proyectil de un objeto disparado en ángulo $ theta _0 $ a horizontal
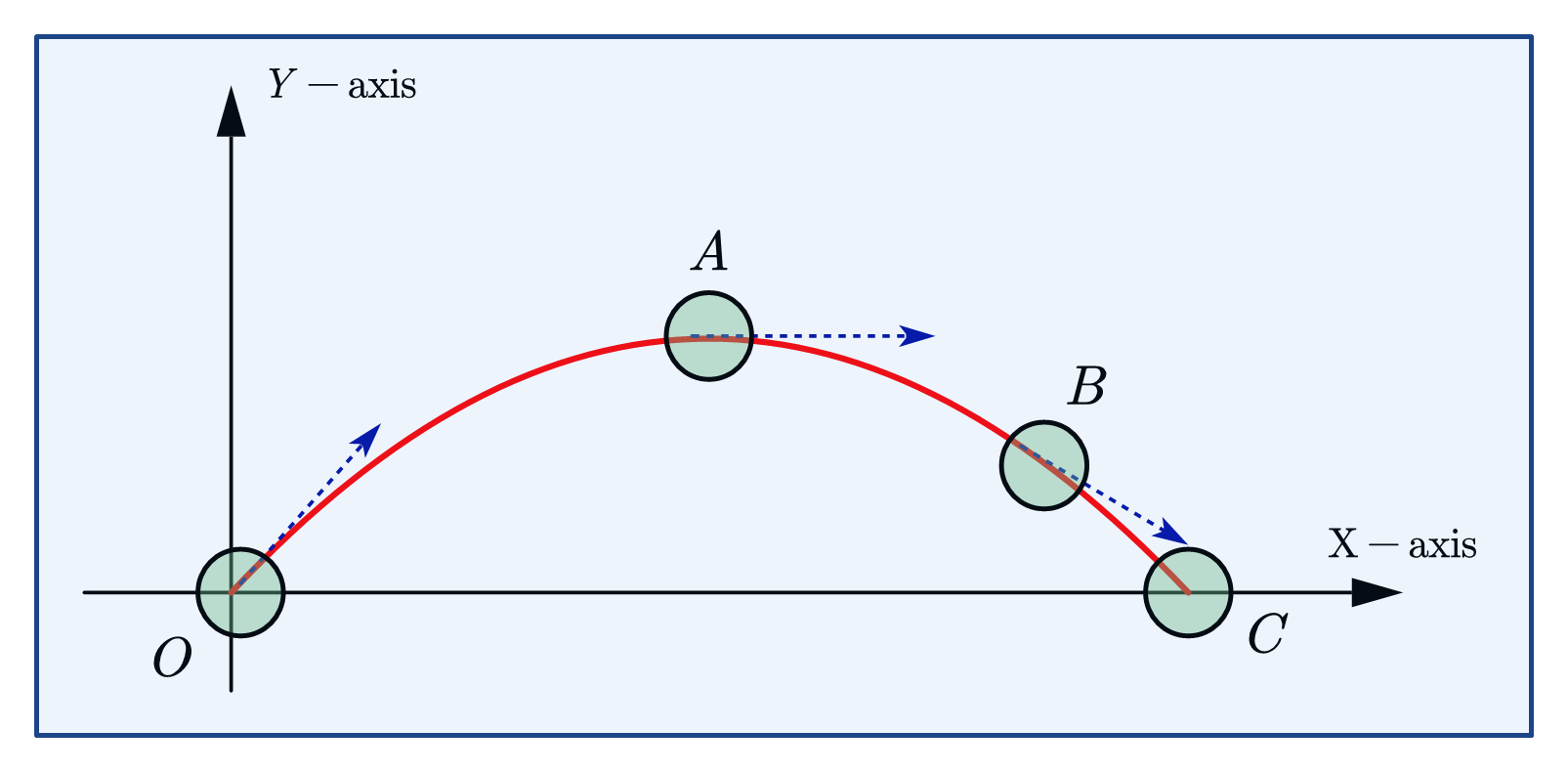
Velocidad inicial Componente horizontal $ {v_ {0x}} = {v_0} cos { theta _0} $ Componente vertical $ {v_ {0y}} = {v_0} sin { theta _0} $
Aceleración horizontal $ a_x = 0 $ Aceleración vertical $ a_y = -g $
Ecuación de movimiento Coordenada X en cualquier punto $ x = (v_0cos { theta _0}) t $ Coordenada Y en cualquier punto $ y = (v_0sin { theta _0}) t- frac {1} {2} gt ^ 2 $ Componente horizontal en cualquier punto $ v_x = v_0cos { theta _0} $ Componente vertical en cualquier punto $ v_y = {v_0} sin { theta _0} -gt $ Ecuación de trayectoria $ y = (tan { theta _0}) x-[frac {g}{2(v_0cos{theta _0})^2}]x ^ 2 $ Esta es la ecuación de la parábola. Tiempo de vuelo del proyectil $ T = frac {2v_0 sin { theta _0}} {g} $ Altura máxima alcanzada por proyectil $ H = frac {v_0 ^ 2 sin ^ 2 { theta _0}} {2g} $ Alcance horizontal del proyectil $ R = frac {v_0 ^ 2 sin {2 { theta _0}}} {g} $ Casos especiales a. El rango máximo para una velocidad inicial dada se obtiene cuando $ theta _0 = 45 ^ 0 $. El rango máximo se da como $ R_m = frac {v_0 ^ 2} {g} $ Ejemplo : Se patea una pelota a una velocidad de 18 m / s en un ángulo de 30 ° con respecto a la horizontal. Encuentra el tiempo de vuelo de la pelota, el alcance de la pelota. Tomar $ g = 10m / s ^ 2 $ Solución Aquí $ v_0 = 18 m / s $ $ theta _0 = 30 $ $ T = frac {2v_0 sin { theta _0}} {g} $ $ T = frac {2 veces 18 veces .5} {10} = 1.8 segundos $ $ R = frac {v_0 ^ 2 sin {2 { theta _0}}} {g} $ $ R = frac {18 ^ 2 times sqrt {3}} {2 times 10} = 28.05 m $






