Ya sabemos sobre el campo eléctrico y el potencial eléctrico. También sabemos que el campo electrostático se caracteriza completamente por la función vectorial
E((
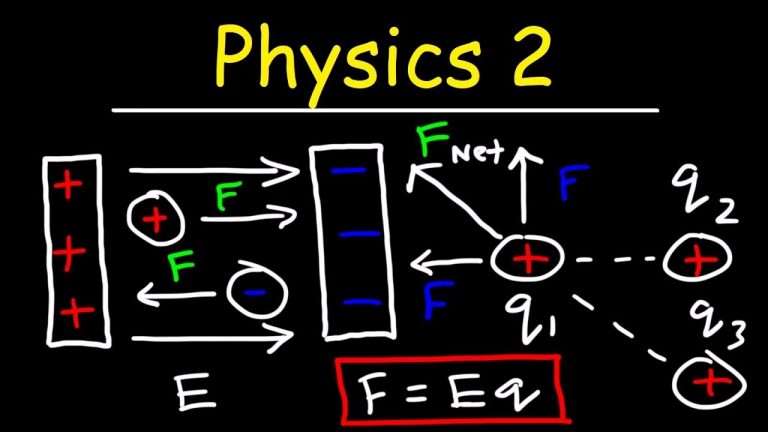
r) El campo eléctrico representa la fuerza ejercida sobre otros objetos cargados eléctricamente por la partícula cargada eléctricamente que rodea el campo. Ahora surge una pregunta por qué necesitamos la introducción del potencial eléctrico cuando ya tenemos un campo eléctrico para la descripción de la fuerza eléctrica entre cargas. En primer lugar, el concepto de potencial eléctrico es muy útil no solo en física sino también en ingeniería, ya que si conocemos el potencial podemos calcular fácilmente el trabajo realizado por las fuerzas de campo cuando una carga se desplaza del punto 1 al punto 2. eso es [{W_{12}} = q({varphi _1} – {varphi _2})] donde ({ varphi _1} ) y ({ varphi _2} ) son los potenciales en los puntos 1 y 2. Esto significa que el trabajo requerido es igual a la disminución de la energía potencial de carga q cuando se desplaza del punto 1 al 2.
El cálculo del trabajo de las fuerzas de campo con la ayuda de la fórmula mencionada anteriormente no es solo simple, sino el único método posible en algunos casos. En segundo lugar, en algunos casos de cálculo de campo electrostático, a menudo es más fácil calcular primero el potencial y luego encontrar el gradiente de potencial ({ varphi} ) para calcular el valor de la intensidad del campo eléctrico E. También para calcular ({ varphi} ) solo necesitamos evaluar una integral pero para calcular E debemos tomar tres integrales todas para direcciones x, y y z ya que E es una cantidad vectorial Pero debemos tener en cuenta que para problemas con alta simetría debemos calcular directamente E utilizando El teorema de Gauss que es una forma mucho más simple de encontrar la intensidad del campo eléctrico cuando la distribución de carga es simétrica