Verificación de resultados en geometría usando cálculo

Las fórmulas utilizadas en Geometría son las siguientes:

Área de un triángulo = 0.5 base altura

Circunferencia de un círculo = 2 pi r

Área de un círculo = pi r r

Verifiquemos cada uno de estos utilizando cálculo, primero verifiquemos el área de un triángulo.

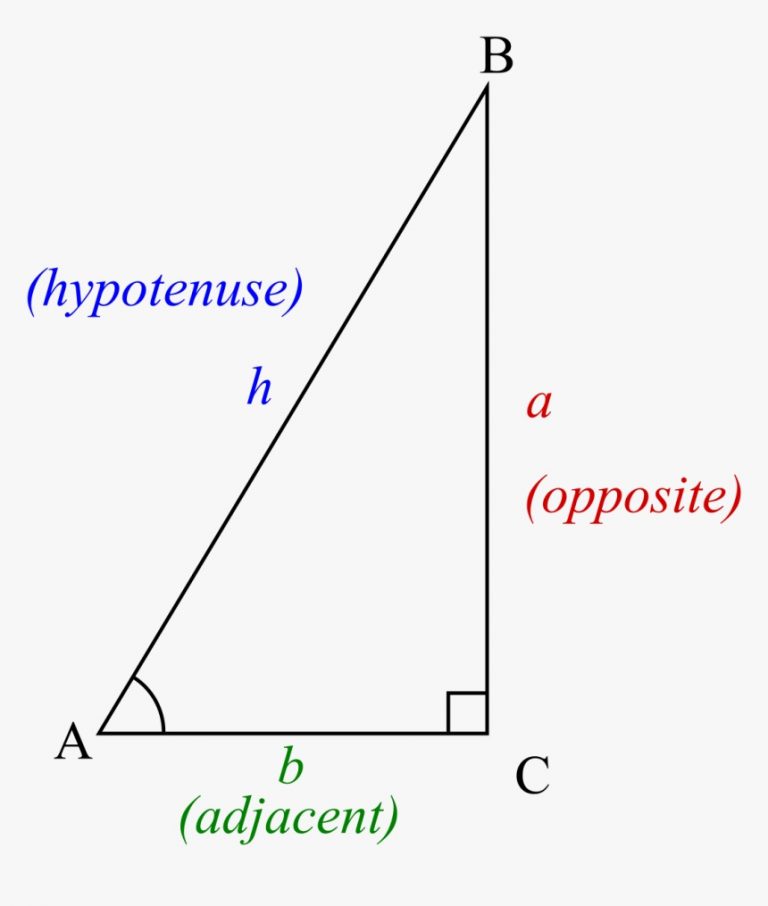
Tomemos un triángulo escaleno ABC y dibujemos una línea recta desde uno de los vértices hacia el lado opuesto, de modo que se encuentre con el lado opuesto en ángulo recto con la base. En esencia, hemos dividido el triángulo original en dos triángulos en ángulo recto.

Derivemos una expresión para el área de un triángulo usando la ecuación de la línea recta como Y = m X + C.; Primero, definamos el área del triángulo como la suma de dos áreas encerradas por los dos lados del triángulo, la altitud y la base. La altitud corta la base en dos pedazos.

Tomemos un triángulo escaleno cuya altitud es 5 y la base es 10. Sea el punto de intersección de la altitud con la base el origen o (0,0). Si los tres vértices son A, B y C respectivamente, entonces si el punto de intersección de la altitud desde el punto A y la línea BC está en D, entonces las coordenadas del punto A son (0.5), el punto B es ( 4,0) y el punto C es (-6,0). La longitud de los tres lados es BC = 10; AC = sqrt (61) aproximadamente igual a 7.8 y AB = sqrt (41) aproximadamente igual a 6.4.

Estos tres puntos forman un triángulo como AB + BC & gt; C.A; AC + BC & gt; AB; AC + AB & gt; ANTES DE CRISTO. Además, como los tres lados del triángulo no son iguales, el triángulo es escaleno.

El área de este triángulo es 0.5 base altura = 0.5 10 5 = 25 unidades cuadradas.

Verifiquemos esto usando cálculo integral.

La pendiente del lado AB es -tan (ABD) o -tan (ABC) que es igual a -1. 25. La ecuación de la línea AB es Y = 5 – 1. 25 X. De manera similar, la ecuación de la línea AC es Y = 5X / 6 + 5. Integremos ambas expresiones entre los límites apropiados.

El área encerrada por la línea AB es integral (Ydx) entre x = 0 yx = 4.

Integral (Ydx) no es más que 5X – 1. 25 X X / 2. Entre los límites, el área es 20 – 10 = 10 .

De manera similar, el área encerrada por la línea AC y el origen es Integral (5x / 6 + 5) dx, que es igual a 5 X X / 12 + 5 X. Los límites de la integración son de 0 a -6, que se evalúa como 15 – 30 o – 15. Tomando el valor absoluto, la suma de ambas áreas es 15 + 10 que es igual a 25. Esto coincide fácilmente con la expresión analítica para el área del triángulo que se evalúa como 25 unidades cuadradas.

Derivemos la expresión para la circunferencia de un círculo. Si se considera un pequeño sector del área d (theta). El área del sector sería r sin (d (theta)). Esto puede ser aproximado a r d (theta) para valores pequeños de d (theta). Si uno integra esta expresión entre 0 y 2 pi, esto resulta ser 2 pi r. Esta expresión equivale a la expresión bien conocida para la circunferencia de un círculo.

Del mismo modo, procedamos a evaluar la expresión del Área del círculo. Calculemos la longitud del arco encerrado por un ángulo pequeño (theta). La circunferencia no es más que r d (theta). El área del sector se puede aproximar al área de un triángulo como 0.5 r r d (theta). Al integrar la expresión 0.5 r r d (theta) entre 0 y 2 pi, se evalúa como pi r r que coincide con la expresión para el área del triángulo.