Modelado matemático de pasos en BharathaNatyam

El modelado matemático implica la creación de un modelo de un sistema del mundo real utilizando técnicas en matemáticas como programación lineal, ecuaciones diferenciales, etc. Un sistema dinámico (System in Motion).

Adavus en BharathaNatyam (forma de arte de danza clásica del sur de India) representa un conjunto de pasos que no implican expresión (nrityam). Entonces Adavus puede estudiarse usando modelos matemáticos.

Tattu Adavu implica levantar los pies hacia arriba y hacia abajo para que uno pueda escuchar el ruido del golpeteo.

El & quot; sollukattu & quot; (palabra tamil traducida al inglés como pronunciación verbal de latidos) se representa en diferentes tempos. También hay movimientos repetidos de los pies en varios recuentos, como 4,6 y 8.

Los cuatro latidos verbales se pueden pronunciar como tai, ya, tai, hola. Si los cuatro latidos verbales ocurren en T (1), T (2), T (3) y T (4) donde T (I) es el i-ésimo instante de tiempo cuando el artista acompañante pronuncia el latido verbal.

La velocidad o el tempo viene dado por T (2) – T (1) T (3) – T (2) y T (4) – T (3). Idealmente, todos estos intervalos de tiempo deberían ser iguales. Puede ser igual si estos latidos se generan a máquina. Pero cuando un artista presenta estos sonidos o ritmos, los intervalos no serán uniformes y variarán al azar. Dichas variaciones pueden capturarse utilizando modelos de simulación.

Si todo el paso del movimiento hacia arriba y hacia abajo de los pies una vez toma 30 segundos (por ejemplo) a velocidad normal. Tomaría 20 segundos y 10 segundos en el segundo y tercer tempos. Por ejemplo, si tai ocurre en el 0º instante, ya ocurre en el 13. 5 segundos, tai es el tiempo de espera durante 3 segundos y hola ocurre en el 30 segundo, el movimiento hacia arriba de los pies dura 13. 5 segundos y el movimiento hacia abajo dura 13. 5 segundos y el tiempo de espera dura 3 segundos. Una bailarina y un vocalista no pueden hacer que el movimiento uniforme sea tan exacto como lo demuestra el modelo matemático y puede haber variaciones.

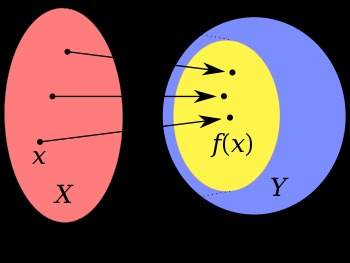
El movimiento del bailarín o artista (#) puede modificarse por la posición del torso en el espacio o x, y, z co- ordena y el movimiento relativo de los pies, piernas, mano superior, mano inferior, brazos, cabeza, cuello y ojos con respecto al torso.

Para una secuencia de pasos de Tattu Adavu que comienzan en el tiempo t = 0 y terminan en el tiempo t = T, la ecuación de los pies en un momento instantáneo t viene dada por la posición del tanco del bailarín y el posición relativa de los pies con respecto al torso.

Dado que Tattu Adavu implica tocar los pies y mover hacia arriba, el movimiento resultante de decir los dedos de los pies puede modificarse usando álgebra usando las siguientes ecuaciones de tiempo discretas que resultan en funciones de pasos que describen el movimiento. Las ecuaciones diferenciales no se pueden utilizar, ya que representarían un sistema continuo.

Escribiendo estas ecuaciones del Tattu Adavu como y = 0 en t = 0 y = h en t = T / 2 e y = 0 en t = T donde T es el período de tiempo de un latido y h es la altura máxima alcanzada por un pie. Esto se puede fijar en 30 cms o se puede variar entre 25 cms y 50 cms. Este es el modelo algebraico del primer Tattu Adavu. En caso de que se vaya a utilizar un modelo de variación, el modelo algebraico utilizado se debe reemplazar por un modelo de simulación.

El segundo tattu adavu o el golpeteo de los pies con dos veces por latido se puede modelar como y = 0 en t = 0 y = h en t = T / 4; y = 0 en t = T / 2; y = h en t = 3T / 4; y = 0 en t = T.

Si el lugar geométrico de los pies se traza para un mayor número de puntos a lo largo del intervalo de tiempo, entonces la misma ecuación se puede describir como y = 0 en t = 0; y = h / 10 y t = T / 10; y = h / 9 en t = T / 9 etc.

Un bailarín con movimiento natural no podrá replicar la congruencia matemática exacta de la altura alcanzada por los pies en movimiento con respecto a las divisiones dentro El período de tiempo del Sollukattu.

Si uno traza el movimiento real de los pies de un bailarín mientras realiza el tattu adavu (traducido al inglés como golpeteo de los pies) la ecuación resultante sería h = 0 en t = 0, y = 0.6h en t = T / 2 y h = 1.1h en t = T, etc.

) Estas ecuaciones algebraicas se pueden usar para escribir programas de computadora que usan gráficos para modelar el movimiento de los pies de un bailarín clásico. Por lo tanto, algunos aspectos de los pasos mecánicos o adavus se pueden generar automáticamente en función del uso de modelos apropiados para capturar el movimiento de los pies.