Geometría intercalada con álgebra
Estudiemos algunas propiedades derivadas de la geometría usando álgebra.
Tomemos el ejemplo de una línea recta. ¿Qué observamos? Una línea recta cruza el eje X o el eje Y en uno de los cuatro cuadrantes. Se puede trazar una línea colgando en algún lugar en el medio, pero arrastrarla de cualquier manera la haría ciertamente intersectarse en uno de los cuatro cuadrantes. ¿Cuáles son las propiedades de una línea recta? Una línea recta intersecta el eje x o el eje y con un ángulo. Si esta línea forma un ángulo de 90 grados con el eje X, entonces es paralela al eje Y o al propio eje Y. Por el contrario, si esta línea forma un ángulo de 90 grados con el eje Y, entonces corre paralela al eje X o puede ser el propio eje X.
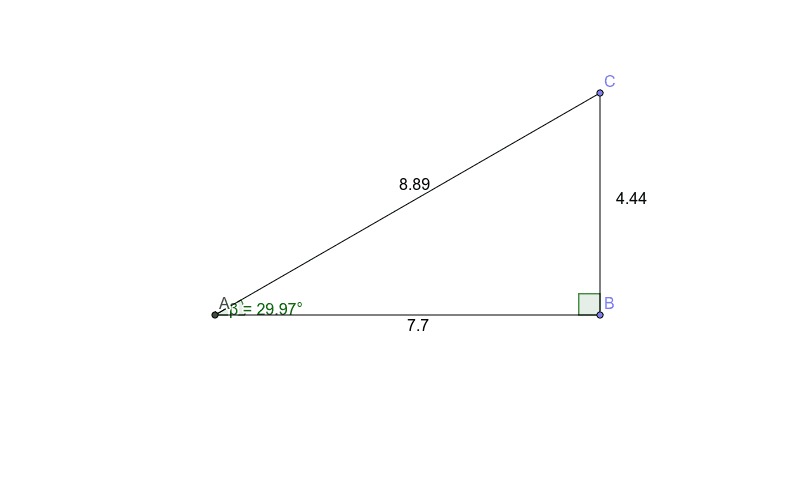
Tomemos un punto en la línea como (X, Y), investiguemos la relación entre X e Y. Proyectemos el punto en los ejes X e Y, respectivamente. Deje que la línea se cruce en el eje X en algún punto (C1,0) y el eje Y en el punto (0, C).
Consideremos el triángulo rectángulo entre el origen y los dos puntos de intersección en el eje X y el eje Y (donde la línea recta se encuentra con los dos ejes. Sea theta el ángulo formado por la línea recta y el Eje X. Por definición, tan (theta) es igual a la altura / base de un triángulo rectángulo. Entonces, tan (theta) en este caso no es más que C / C1.
En cualquier otro punto (X, Y) en la línea recta tan (theta) es igual a Y / C1-X.
Al igualar ambos obtenemos Y / C1-X = C / C1, entonces Y = C (C1-X) / C1 = -XC / C1 + C.
Dado que theta es el ángulo interior formado por la línea recta con el eje X, el ángulo exterior es igual a PI-Theta. Además, tan (theta) = – tan (PI-theta).
Entonces, si sigue que -C / C1 = tan (ángulo exterior).
Y = tan (ángulo exterior) X + C. Esto es solo la ecuación popular Y = M X + C.
Ahora apliquemos un poco de álgebra elemental para derivar el pythogoreas teorema.
Consideremos un triángulo rectángulo en el origen con coordenadas (0,0), (a, 0) y (0, b)
La longitud de la hipotenusa no es más que sqrt (a a + b b).
Esta es solo la suma de los cuadrados de los otros dos lados, que es según Pythogoreas teorema.
Ahora pasemos a un círculo, cuáles son las propiedades de un círculo. Cualquier punto a lo largo del círculo está a una distancia de r desde el centro del círculo. Deje que el centro del círculo esté en el origen. Tomemos un punto (X, Y) ubicado en cualquier punto de un círculo. Entonces, la distancia de ese punto al centro no es nada sqrt (X X + Y Y), que es igual a r la longitud del radio.
Entonces la ecuación de un círculo es sqrt (X X + Y Y) = ro X X + Y Y = r r.
La aplicación de álgebra a la geometría se denomina popularmente como geometría coordinada.